近似差分隐私

学习目标

阅读本章后，您将能够：

• 定义近似差分隐私

• 解释近似差分隐私和纯粹差分隐私的区别

• 描述近似差分隐私的优势和劣势

• 描述和计算向量值查询的L1和L2敏感度

• 定义和使用高斯机制

• 应用高级组合性

近似差分隐私（Approximate Differential Privacy）[5]，也称\((\epsilon, \delta)\)-差分隐私，其定义如下所述：

(6)\[\begin{align} \mathsf{Pr}[F(x) = S] \leq e^\epsilon \mathsf{Pr}[F(x') = s] + \delta \end{align}\]

新出现的隐私参数\(\delta\)表示不满足此近似差分隐私定义的”失败概率”。我们有\(1-\delta\)的概率获得等价于纯粹差分隐私的隐私保护程度。同时，我们有\(\delta\)的概率不满足隐私参数为\(\epsilon\)的纯粹差分隐私。换句话说：

• 满足\(\frac{\mathsf{Pr}[F(x) = S]}{\mathsf{Pr}[F(x') = s]} \leq e^\epsilon\)的概率为\(1-\delta\)

• 不能保证满足上述不等式的概率为\(\delta\)

上述定义看起来有点吓人！我们有\(\delta\)的概率无法保证差分隐私，这意味着我们甚至可能有\(\delta\)的概率泄露整个敏感数据集！因此，我们通常要求\(\delta\)很小。一般来说，我们要求\(\delta\)的取值小于等于\(\frac{1}{n^2}\)，其中\(n\)表示数据集的总大小。此外，我们还将看到，实际使用的\((\epsilon, \delta)\)-差分隐私机制不会像定义所描述的那样吓人，不会出现一旦失败就引发灾难性后果的情况。实际上，该机制会温和地失败，一般不会造成诸如泄露整个数据集之类的严重后果。

确实可以构造出此类机制，并可以证明构造出的机制确实满足\((\epsilon, \delta)\)-差分隐私。我们将在本章后续部分看到实际的机制构造方法。

近似差分隐私的性质

近似差分隐私拥有和纯粹\(\epsilon\)-差分隐私相似的特性。它同样满足串行组合性：

• 如果\(F_1(x)\)满足\((\epsilon_1, \delta_1)\)-差分隐私

• 同时\(F_2(x)\)满足\((\epsilon_2, \delta_2)\)-差分隐私

• 则发布两个结果的机制\(G(x) = (F_1(x), F_2(x))\)满足\((\epsilon_1+\epsilon_2, \delta_1 + \delta_2)\)-差分隐私

与纯粹\(\epsilon\)-差分隐私相比，近似差分隐私串行组合性唯一的不同之处在于需要分别对\(\delta\)和\(\epsilon\)相加。近似差分隐私同样满足后处理性和并行组合性。

高斯机制

可以用高斯机制替代拉普拉斯机制。高斯机制增加的不是拉普拉斯噪声，而是高斯噪声。高斯机制无法满足纯粹\(\epsilon\)-差分隐私，但可以满足\((\epsilon, \delta)\)-差分隐私。对于一个返回数值的函数\(f(x)\)，应用下述定义的高斯机制，可以得到满足\((\epsilon, \delta)\)-差分隐私的\(F(x)\)：

(7)\[\begin{align} F(x) = f(x) + \mathcal{N}(\sigma^2)\\ \text{where } \sigma^2 = \frac{2s^2 \log(1.25/\delta)}{\epsilon^2} \end{align}\]

其中\(s\)是\(f\)的敏感度，\(\mathcal{N}(\sigma^2)\)表示均值为0，方差为\(\sigma^2\)的高斯（正态）分布采样结果。请注意，这里的\(\log\)表示自然对数（本书其他地方出现的\(\log\)同样表示自然对数）。

对于实值函数\(f : D \rightarrow \mathbb{R}\)，我们可以按照与拉普拉斯机制完全相同的方法使用高斯机制。在相同的\(\epsilon\)取值下，很容易对比两种机制的应用效果。

Show code cell source Hide code cell source

epsilon = 1
vals_laplace = [np.random.laplace(loc=0, scale=1/epsilon) for x in range(100000)]

delta = 10e-5
sigma = np.sqrt(2 * np.log(1.25 / delta)) * 1 / epsilon
vals_gauss = [np.random.normal(loc=0, scale=sigma) for x in range(100000)]

plt.hist(vals_laplace, bins=50, label='拉普拉斯')
plt.hist(vals_gauss, bins=50, alpha=.7, label='高斯');
plt.legend();

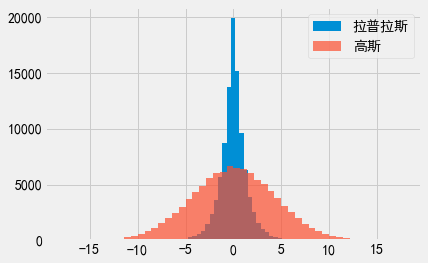
这里我们画出了\(\epsilon = 1\)时，拉普拉斯机制和高斯机制的经验概率密度函数，我们这里令高斯机制的\(\delta = 10^{-5}\)。

与拉普拉斯机制的曲线相比，高斯机制的曲线看起来更”平”。当应用高斯机制时，我们更有可能得到远离真实值的差分隐私输出结果，而拉普拉斯机制的输出结果与真实值更接近一些（相比之下，拉普拉斯机制的曲线看起来更”尖”）。

因此，高斯机制有两个严重的缺点：其一，该机制需要使用宽松的\((\epsilon, \delta)\)-差分隐私定义；其二，该机制的准确性不如拉普拉斯机制。既然如此，为什么我们还需要高斯机制呢？

向量值函数及其敏感度

截至目前，我们考虑的都是实值函数（即输出总为单一实数的函数）。此类函数的形式为：\(f : D \rightarrow \mathbb{R}\)。拉普拉斯机制和高斯机制都可以扩展到形式为：\(f : D \rightarrow \mathbb{R}^k\)的向量值函数，即输出为实数向量的函数。我们可以将直方图看作向量值函数，其返回的向量表示直方图各个分箱的计数值。

我们在前面提到，函数的敏感度定义为：

(8)\[\begin{align} GS(f) = \max_{d(x,x') \leq 1} \lvert f(x) - f(x') \rvert \end{align}\]

我们如何定义向量值函数的敏感度呢？

考虑表达式\(f(x) - f(x')\)。如果\(f\)是向量值函数，那么该表达式表示的是两个向量之间的差，可以通过计算对应位置元素之间的差来得到（两个长度为\(k\)的向量差是一个长度为\(k\)的新向量）。这个新向量就是\(f(x)\)和\(f(x')\)之间的距离。

该向量的标量长度就是\(f\)的敏感度。有很多计算向量标量长度的方法。我们将使用两种方法：\(L1\)范数和\(L2\)范数。

L1和L2范数

给定长度为\(k\)的向量\(V\)，其\(L1\)范数定义为\(\lVert V \rVert_1 = \sum_{i=1}^k \lvert V_i \rvert\)（即向量各个元素的和）。在二维空间中，两个向量之差的\(L1\)范数就是它们的”曼哈顿距离”。

给定长度为\(k\)的向量\(V\)，其\(L2\)范数定义为\(\lVert V \rVert_2 = \sqrt{\sum_{i=1}^k V_i^2}\)（即向量各个元素平方和再求平方根）。在二维空间中，两个向量之差的\(L2\)范数就是它们的”欧氏距离”。\(L2\)范数总是小于或等于\(L1\)范数。

L1和L2敏感度

向量值函数\(f\)的\(L1\)敏感度为：

(9)\[\begin{align} GS(f) = \max_{d(x,x') \leq 1} \lVert f(x) - f(x') \rVert_1 \end{align}\]

此敏感度等于向量各个元素敏感度的和。举例来说，如果我们定义了一个向量值函数\(f\)，其返回一个长度为\(k\)的向量，且向量中各个元素的敏感度均为1，则\(f\)的\(L1\)敏感度为\(k\)。

类似地，向量值函数\(f\)的\(L2\)敏感度为：

(10)\[\begin{align} GS_2(f) = \max_{d(x,x') \leq 1} \lVert f(x) - f(x') \rVert_2 \end{align}\]

同样是上述的例子，向量值函数\(f\)返回一个长度为\(k\)的向量，且向量中各个元素的敏感度均为1，则\(f\)的\(L2\)敏感度为\(\sqrt{k}\)。对于长向量，\(L2\)敏感度显然比\(L1\)敏感度低得多！在机器学习算法（返回的向量有时包含成千上万个元素）等应用中，\(L2\)敏感度显著低于\(L1\)敏感度。

选择L1还是L2

如之前所述，拉普拉斯机制和高斯机制都可以扩展到向量值函数。然而，这两种机制的扩展结果间有一个关键差异点：向量值拉普拉斯机制需要使用\(L1\)敏感度，而向量值高斯机制既可以使用\(L1\)敏感度，也可以使用\(L2\)敏感度。这是高斯机制的一个重要优势。对于\(L2\)敏感度远低于\(L1\)敏感度的应用来说，高斯机制添加的噪声要小得多。

• 向量拉普拉斯机制发布的是\(f(x) + (Y_1, \dots, Y_k)\)，其中\(Y_i\)是采样自拉普拉斯分布的独立同分布噪声，噪声尺度为\(\frac{s}{\epsilon}\)，其中\(s\)是\(f\)的\(L1\)敏感度。

• 向量高斯机制发布的是\(f(x) + (Y_1, \dots, Y_k)\)，其中\(Y_i\)是采样自高斯分布的独立同分布噪声，且\(\sigma^2 = \frac{2s^2 \log(1.25/\delta)}{\epsilon^2}\)，其中\(s\)是\(f\)的\(L2\)的敏感度。

灾难机制

\((\epsilon, \delta)\)-差分隐私定义称，满足此差分隐私定义的机制必须以\(1-\delta\)的概率”表现良好”。但这也意味着此机制可以有\(\delta\)的概率执行任何操作。”失败概率”的存在令人无比担忧，因为满足宽松定义的差分隐私机制总可能（即使发生的概率很低）给出糟糕的输出结果。

考虑如下机制，我们称之为灾难机制（Catastrophe Mechanism）：

(11)\[\begin{align} F(q, x) =\;& \text{在0到1之间均匀随机地采样得到一个数$r$}\\ &\text{如果 } r < \delta, \text{返回 } x\\ &\text{否则，返回 } q(x) + \text{Lap}(s/\epsilon), \text{其中$s$是$q$的敏感度}\\ \end{align}\]

灾难机制有\(1-\delta\)的概率满足\(\epsilon\)-差分隐私。然而，灾难机制同时有\(\delta\)的概率泄露无噪声的整个数据集。尽管该机制满足近似差分隐私定义，但我们在实际中不太可能会应用此机制。

幸运的是，大多数\((\epsilon, \delta)\)-差分隐私机制不会出现类似的灾难性失效情况。例如，高斯机制就不会真的发布整个数据集。高斯机制只是有\(\delta\)的概率不会严格地满足\(\epsilon\)-差分隐私，而是满足某个值\(c\)下的\(c\epsilon\)-差分隐私。

因此，高斯机制会很温和地失败，而不会灾难性地失败。因此，与灾难机制相比，我们有理由相信高斯机制可以为我们提供更好的隐私保护。我们后续还将看到差分隐私的另一种宽松定义方法。此定义可以区分温和性失败机制（如高斯机制）和灾难性失败机制（如灾难机制）。

高级组合性

我们已经学习了差分隐私机制的两种组合方式：串行组合性和并行组合性。事实证明，\((\epsilon, \delta)\)-差分隐私引入了差分隐私机制串行组合性的一种新分析方法，此分析方法可以进一步降低隐私消耗量。

高级组合定理[7]通常用\(k\)-折叠适应性组合（\(k\)-fold Adaptive Composition）机制来描述。\(k\)-折叠适应性组合指的是将一系列机制\(m_1, \dots, m_k\)组合起来，这些机制满足下述条件：

• 适应性：可以根据所有前述机制\(m_1, \dots, m_{i-1}\)的输出来选择下一个机制\(m_i\)

• 组合性：每个机制\(m_i\)的输入既包括隐私数据集，也包括前述机制的所有输出

迭代程序（如循环或递归函数）几乎都是\(k\)-折叠适应性组合的实例。例如，一个执行1000轮的for循环是1000-折叠适应性组合。再举一个更特殊的例子，平均攻击也是\(k\)-折叠适应性组合：

# 此攻击针对的是敏感度为1的问询
def avg_attack(query, epsilon, k):
    results = [query + np.random.laplace(loc=0, scale=1/epsilon) for i in range(k)]
    return np.mean(results)

avg_attack(10, 1, 500)

9.95822939104013

在这个例子中，我们提前确定好了机制的组合顺序（我们每次都使用相同的机制），且\(k = 500\)。

标准串行组合定理称，该机制的总隐私消耗量为\(k\epsilon\)（本例的总隐私消耗量为\(500 \epsilon\)）。

高级组合定理称：

• 如果\(k\)-折叠适应性组合\(m_1, \dots, m_k\)中的每一个机制\(m_i\)都满足\(\epsilon\)-差分隐私

• 则对于任意\(\delta \geq 0\)，整个\(k\)-折叠适应性组合满足\((\epsilon', \delta')\)-差分隐私，其中：

(12)\[\begin{align} \epsilon' = 2\epsilon \sqrt{2k \log(1/\delta')} \end{align}\]

根据前面的例子，将\(\epsilon = 1\)代入到表达式中，并设置\(\delta' = 10^{-5}\)，我们有：

(13)\[\begin{align} \epsilon' =& 2 \sqrt{1000 \log(100000)}\\ \approx& 214.59 \end{align}\]

因此，对于相同机制，应用高级组合性得到的\(\epsilon'\)下界远低于应用串行组合性得到的下界。这意味着什么呢？这意味着串行组合性得到的隐私消耗量下界是宽松的。与实际隐私消耗相比，串行组合性得到的下界不够紧致。事实上，高级组合性得到的下界也是宽松的，此下界只是比串行组合性给出的下界稍显紧致一些。

需要着重强调的是，得到的两种隐私消耗量上界在技术角度看不具有可比性，因为高级组合性引入了\(\delta\)。但当\(\delta\)很小时，我们通常可以比较两种方法给出的\(\epsilon\)。

既然如此，我们应该总是使用高级组合性吗？并非如此。我们分别对于不同的\(k\)值计算隐私消耗量，绘制串行组合性和高级组合性的总隐私消耗图。

Show code cell source Hide code cell source

epsilon = 1
delta = 10e-5

def adv_comp(k):
    return 2*epsilon*np.sqrt(2*k*np.log(1/delta))

def seq_comp(k):
    return k*epsilon

plt.plot([seq_comp(k) for k in range(100)], label='串行组合性')
plt.plot([adv_comp(k) for k in range(100)], label='高级组合性')
plt.legend();

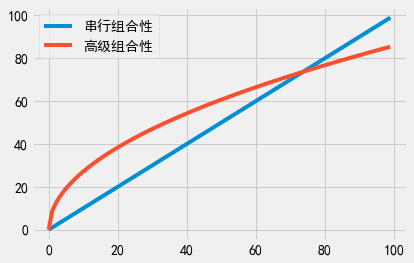
事实证明，当\(k\)小于70时，标准的串行组合性比高级组合性得到的总隐私消耗量更小。因此，仅当\(k\)比较大时（如大于100时），高级组合性才会有用武之地。不过，当\(k\)非常大时，高级组合性可以显露出巨大的优势。

Show code cell source Hide code cell source

plt.plot([seq_comp(k) for k in range(10000)], label='串行组合性')
plt.plot([adv_comp(k) for k in range(10000)], label='高级组合性')
plt.legend();

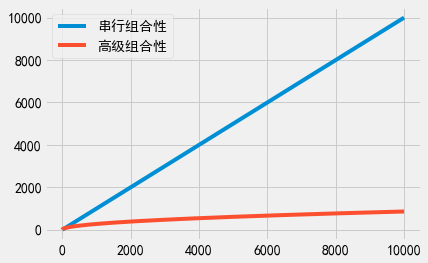
近似差分隐私的高级组合性

当使用高级组合性时，前述要求各个机制均需满足纯粹\(\epsilon\)-差分隐私。然而，如果各个机制满足\((\epsilon, \delta)\)-差分隐私，高级组合定理同样适用。高级组合定理更一般的描述如下（[7], 定理3.20）：

• 如果\(k\)-折叠适应性组合\(m_1, \dots, m_k\)中的每个机制\(m_i\)都满足\((\epsilon, \delta)\)-差分隐私

• 则对于任意\(\delta' \geq 0\)，整个\(k\)-折叠适应性组合都满足\((\epsilon', k\delta + \delta')\)-差分隐私，其中：

(14)\[\begin{align} \epsilon' = 2\epsilon \sqrt{2k \log(1/\delta')} \end{align}\]

与前面的描述相比，唯一的区别是组合机制的失败参数\(\delta\)，即这里的失败参数包含额外的\(k\delta\)项。当待组合的机制满足纯粹\(\epsilon\)-差分隐私时，我们有\(\delta = k\delta = 0\)。两种描述在纯粹差分隐私下得到的结果一致。